Question
Given an unsorted integer array, find the first missing positive integer.
For example,
Given [1,2,0] return 3,
and [3,4,-1,1] return 2.
Your algorithm should run in O(n) time and uses constant space.
Stats
| Frequency | 2 |
| Difficulty | 5 |
| Adjusted Difficulty | 4 |
| Time to use | -------- |
Ratings/Color = 1(white) 2(lime) 3(yellow) 4/5(red)
Analysis
This is a very difficult question!
The tricky part of this question is the limit in space/time. If we sort and check, the space is constent, but time is increased.
The key is to make use of the position index of the array.
Solution
Make sure that (i)th item of the array stores value (i+1). The image below and the quoted text from this blog are very good explanations.
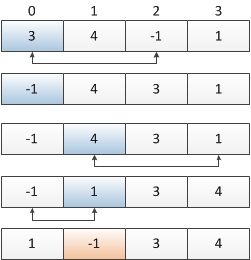
The idea is simple. What is the most desired array we want to see? Something like [1,2,3] then we know 4 is missing, or [1, 8, 3, 4] then we know 2 is missing. In other word, “all the numbers are in their correct positions”.
What are correct positions? For any i, A[i] = i+1. So our goal is to rearrange those numbers (in place) to their correct positions.
We then need to decide how to arrange them. Let’s take the [3, 4, -1, 1] as an example. The 1st number, 3, we know it should stay in position 2. So we swap A[0] = 3 with A[2]. We then get [-1, 4, 3, 1]. We can’t do anything about -1 so we leave it there. The 2nd number, 4, we know it should sit in A[3]. So we swap A[1] = 4 with A[3]. We then get [-1, 1, 3, 4]. Now 1 should stay in A[0], so we keep swapping and we get [1, -1, 3, 4]. Notice now every positive number is staying in their correct position (A[0]=1, A[2]=3 and A[3]=4). We then need one more scan to find out 2 is missing.
My code
public class Solution {
public int firstMissingPositive(int[] A) {
if (A == null || A.length == 0) {
return 1;
}
int len = A.length;
int p = 0;
while (p < len) {
if (A[p] == p + 1) {
// the number is in its correct position~
p++;
continue;
} else if (A[p] <= 0 || A[p] > len) {
// the number is out of range, leave it alone then.
p++;
continue;
} else if (A[p] == A[A[p] - 1]) {
// this is an important case!!! I missed it just now~
p++;
continue;
}
swop(A, p, A[p] - 1);
}
// now check and find the first number that is not in correct position
p = 0;
while (p < len) {
if (A[p] != p + 1) {
return p + 1;
}
p++;
}
return p + 1;
}
private void swop(int[] A, int x, int y) {
int temp = A[x];
A[x] = A[y];
A[y] = temp;
}
}