Question
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
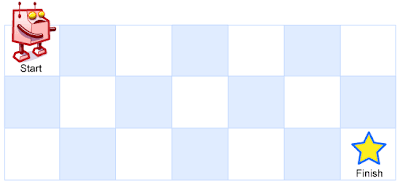
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
Stats
| Frequency | 3 |
| Difficulty | 2 |
| Adjusted Difficulty | 2 |
| Time to use | -------- |
Ratings/Color = 1(white) 2(lime) 3(yellow) 4/5(red)
Solution
This is an easy question.
Basically to walk from (0,0) to (m,n), robot have to walk down (m-1) steps and rightward (n-1) steps. Then this problem simply becomes Number of k-combinations (also known as choose m from n problem). The code is just concise and short.
My code
public class Solution {
public int uniquePaths(int m, int n) {
m--;
n--;
if (m < 0 || n < 0) {
return 0;
} else if (m == 0 || n == 0) {
return 1;
}
long sum = 1;
// the answer would be "choose m from (m + n)"
if (m > n) {
int temp = m;
m = n;
n = temp;
}
int num = m + n;
for (int i = 0; i < m; i++) {
sum *= (num - i);
}
for (int i = 0; i < m; i++) {
sum /= (i + 1);
}
return (int) sum;
}
}