ref

Suffix tree

Both KMP Algorithm and Rabin Karp Algorithm pre-process the pattern to make the pattern searching faster. The best time complexity that we could get by preprocessing pattern is O(n), where n is length of the text.

Now we will discuss an approach that pre-processes the text. A suffix tree is built of the text. After preprocessing text (building suffix tree of text), we can search any pattern in O(m) time where m is length of the pattern.

Though search is very fast - just proportional to length of the pattern, it may become costly if the text changes frequently. It is good for fixed text or less frequently changing text though.

Suffix Tree VS. Trie

A Suffix Tree is a compressed trie of all suffixes of the given text.

Compressed Trie

A Compressed Trie is obtained from standard trie by joining chains of single nodes.

Example, a standard trie:

A Compressed Trie:

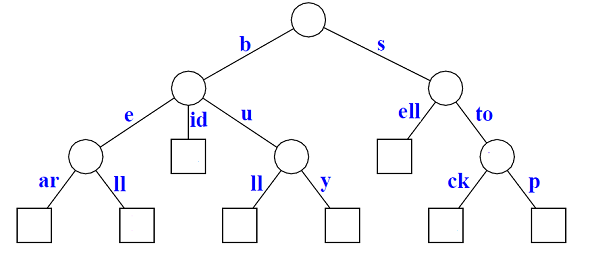
build a Suffix Tree

1. Generate all suffixes of given text.
2. Consider all suffixes as individual words and build a compressed trie.

Eg.

banana\0
anana\0
nana\0
ana\0
na\0
a\0
\0

Example question: [CC150v4] 20.8 Full Text Search (Suffix Tree)