Question
Given stock price of Amazon for some consecutive days. Need to find the maximum span of each day’s stock price.
Definition of ‘span’ have got 2 variant:
Variant 1
Span is the number of consecutive days right before that day, which have less or equal stock value.
(Or in GFG language): The span Si of the stock’s price on a given day i is defined as the maximum number of consecutive days just before the given day, for which the price of the stock on the current day is less than or equal to its price on the given day.
Solution
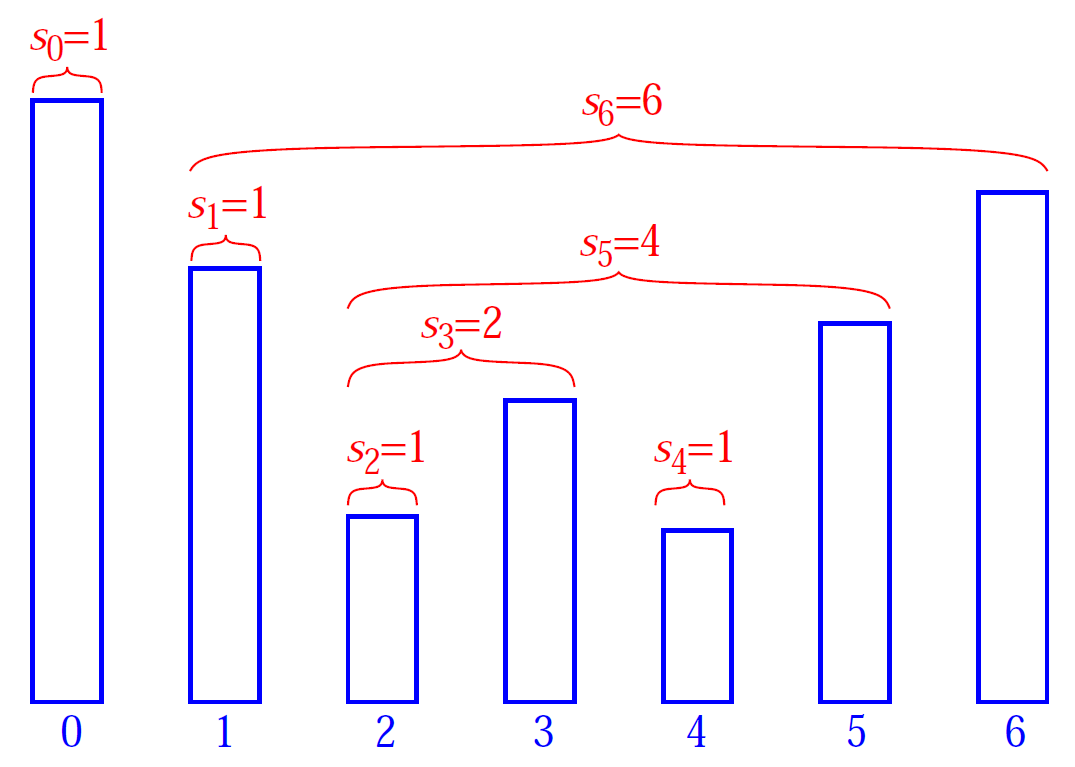
Use stack.
Variant 2
Span is the amount of days before the given day where the stock price is less than that of given day.
Solution
The top answer in here is wrong. Eg. {1,3,2,4}, the count for 4 would be 2, instead of 3.
Instead, the BST (AVL tree) solution is correct. It’s commented by user zahidbuet106.
insert numbers in a AVL tree one by one from right to left. During each insert we will keep updating the size of left subtree at the node being inserted. This will give us our desired smaller element count.
We also need to handle balancing the tree while insert.
The key of this question is the special BST, where each node stores an additional counting number.
This type of special BST is extremely frequntly used in Computer Science, especially when we want to dynamically insert elements and find out it’s ranking within the past history.
Read another very interesting post: [CC150v5] 11.8 Get Rank in Stream of Integers.
Code
class TreeNodePlus extends TreeNode {
int leftCount;
int dupCount;
public TreeNodePlus(int v, int leftC) {
super(v);
this.leftCount = leftC;
this.dupCount = 1;
}
public int findRank(TreeNodePlus node) {
TreeNodePlus leftBranch = (TreeNodePlus) this.left;
TreeNodePlus rightBranch = (TreeNodePlus) this.right;
if (this == node) {
return 0;
} else if (node.val < this.val) {
if (this.left == null) {
return 0;
} else {
return leftBranch.findRank(node);
}
} else {
if (this.right == null) {
return this.leftCount + this.dupCount;
} else {
return this.leftCount + this.dupCount
+ rightBranch.findRank(node);
}
}
}
public TreeNodePlus insertNum(int num) {
TreeNodePlus leftBranch = (TreeNodePlus) this.left;
TreeNodePlus rightBranch = (TreeNodePlus) this.right;
if (num == this.val) {
this.dupCount++;
return this;
} else if (num < this.val) {
// insert num to the left branch
this.leftCount++;
if (this.left == null) {
this.left = new TreeNodePlus(num, 0);
return (TreeNodePlus) this.left;
} else {
return leftBranch.insertNum(num);
}
} else {
// insert num to the right branch
// this.leftCount does not change
if (this.right == null) {
this.right = new TreeNodePlus(num, 0);
return (TreeNodePlus) this.right;
} else {
return rightBranch.insertNum(num);
}
}
}
}