Question

link

Given two line segments (p1, q1) and (p2, q2), check if 2 line segments intersect.

Orientation

Considering 3 pointer, orientation can be:

1. counterclockwise
2. clockwise
3. colinear (not considering direction)

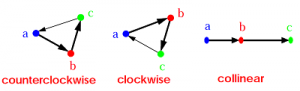
Note that orientation only tells the order and sequence relationship of 3 points. It tells nothing about intersection.

Intersection

Considering 2 line segments: (p1,q1) and (p2,q2).

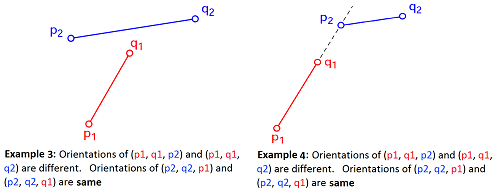
Case 1: general

Two line segment intersect if BOTH the 2 conditions hold:

1. (p1, q1, p2) and (p1, q1, q2) have different orientations and
2. (p2, q2, p1) and (p2, q2, q1) have different orientations

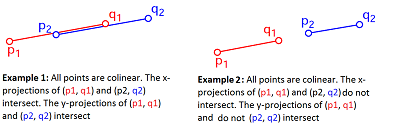
Case 2: special

The speical case is: what if all 4 pointers (p1, q1, p2, q2) are all on the same line!!! Well, this definitely can happen.

If so, check if the values of x-axis and y-axis intersect. I.e. the below 2 cases:

Code

Translated from G4G:

public boolean intersect(Pair p1, Pair q1, Pair p2, Pair q2) {

    int o1 = orientation(p1, q1, p2);
    int o2 = orientation(p1, q1, q2);
    int o3 = orientation(p2, q2, p1);
    int o4 = orientation(p2, q2, q1);

    // General case
    if (o1 != o2 && o3 != o4) {
        // 2 lines intersect
        return true;
    }

    // Special Cases
    Segment seg1 = new Segment(p1, q1);
    Segment seg2 = new Segment(p2, q2);

    // p1, q1 and p2 are colinear and p2 lies on segment p1q1
    if (o1 == 0 && onSegment(seg1, p2))
        return true;

    // p1, q1 and p2 are colinear and q2 lies on segment p1q1
    if (o2 == 0 && onSegment(seg1, q2))
        return true;

    // p2, q2 and p1 are colinear and p1 lies on segment p2q2
    if (o3 == 0 && onSegment(seg2, p1))
        return true;

    // p2, q2 and q1 are colinear and q1 lies on segment p2q2
    if (o4 == 0 && onSegment(seg2, q1))
        return true;

    return false; // Doesn't fall in any of the above cases
}

private boolean onSegment(Segment seg, Pair q) {
    // check if q lies on line segment seg(p1, p2)
    if (q.x <= Math.max(seg.p1.x, seg.p2.x)
            && q.x >= Math.min(seg.p1.x, seg.p2.x)
            && q.y <= Math.max(seg.p1.y, seg.p2.y)
            && q.y >= Math.min(seg.p1.y, seg.p2.y))
        return true;

    return false;
}

private int orientation(Pair first, Pair second, Pair third) {
    int val = (second.y - first.y) * (third.x - second.x)
            - (second.x - first.x) * (third.y - second.y);
    if (val == 0) {
        // colinear
        return 0;
    } else {
        // clock or counterclock wise (1 or -1)
        return val / Math.abs(val);
    }
}

class Segment {
    Pair p1;
    Pair p2;

    public Segment(Pair p1, Pair p2) {
        this.p1 = p1;
        this.p2 = p2;
    }
}

Question

link

Given a binary matrix, find out the maximum size square sub-matrix with all 1s. For example, consider the below binary matrix.

   0  1  1  0  1 
   1  1  0  1  0 
   0  1  1  1  0
   1  1  1  1  0
   1  1  1  1  1
   0  0  0  0  0

The maximum square sub-matrix with all set bits is size 9. Note we only find square, not rectangles! (this makes it much easier)

Solution

Since square only, we can use DP. Quoted answer below:

Let the given binary matrix be M[R][C]. The idea of the algorithm is to construct an auxiliary size matrix S[][] in which each entry S[i][j] represents size of the square sub-matrix with all 1s including M[i][j] where M[i][j] is the rightmost and bottommost entry in sub-matrix.

1. Construct a sum matrix S[R][C] for the given M[R][C].

2. Copy first row and first columns as it is from M[][] to S[][]

3. For other entries, use following expressions to construct S[][]

         If M[i][j] is 1 then
            S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1
         Else /*If M[i][j] is 0*/
            S[i][j] = 0

Question

link

Given set of words that are lexicographically sorted, return lexicographic order. E.g:

abc
acd
bcc
bed
bdc
dab

The order of letters for the given example would be

a->b->c->e->d

Solution

Just form a graph(DAG) and do a topological sort.

Start from the first pair in the dictionary. Compare two strings in this pair till first mismatch.

Eg: aad & aab, in this case create an edge d -> b.

More details is available here.

Variant, and a different solution

Another way of asking this question, is:

有一个字典因为某种原因每个字符都被替换成一个别的字符了（但还是一一对应)， 但是单词的顺序没有改变，比如

cat
coffee
common

--> 

dkc
dbhhzz
dbllbq

让找出的这个替换的规则（guaranteed to have a unique one)

Alternative solution is to check according to frequencies.

Code

public String lexicoOrder(String[] dict) {
    String ans = "";

    // for each pair, maintain 2 HashMap
    HashMap<Character, Integer> incount = new HashMap<Character, Integer>();
    HashMap<Character, List<Character>> connection = new HashMap<Character, List<Character>>();
    for (String str : dict) {
        for (char c : str.toCharArray()) {
            incount.put(c, 0);
            connection.put(c, new ArrayList<Character>());
        }
    }
    buildGraph(dict, incount, connection);

    // start topology sorting
    Queue<Character> temp = new LinkedList<Character>();
    for (char c : incount.keySet()) {
        if (incount.get(c) == 0) {
            temp.offer(c);
            incount.remove(c);
            // remove any node whose incount is 0
        }
    }
    while (!temp.isEmpty()) {
        char top = temp.poll();
        ans += top;
        // 'top' is next char in line. remove it and delete connections
        List<Character> inNodes = connection.get(top);
        for (char c : inNodes) {
            // remove incount for all nodes from inNodes
            incount.put(c, incount.get(c) - 1);
            if (incount.get(c) == 0) {
                incount.remove(c);
                temp.offer(c);
            }
        }
    }
    if (incount.size() == 0)
        return ans;
    else
        return "unable to find a valid char sequence.";
}

public void buildGraph(String[] dict, HashMap<Character, Integer> incount,
        HashMap<Character, List<Character>> connection) {
    // build the graph map
    // abc
    // acd
    // bcc
    // bed
    // bdc
    // dab
    for (int i = 0; i < dict.length - 1; i++) {
        // compare dict[i] and dict[i+1]
        String str1 = dict[i];
        String str2 = dict[i + 1];
        int p = 0;
        while (p < str1.length() && p < str2.length()) {
            if (str1.charAt(p) == str2.charAt(p)) {
                p++;
            } else {
                break;
            }
        }
        if (p == str1.length()) {
            // this is special case eg. "ab" & "abc"
            // this will not give up any information about lexico order
            continue;
        }
        char from = str1.charAt(p);
        char to = str2.charAt(p);
        // update incount
        incount.put(to, incount.get(to) + 1);
        // update connection
        connection.get(from).add(to);
    }
}

Question

link

Given a string, find its rank among all its permutations sorted lexicographically.

For example, rank of “abc” is 1, rank of “acb” is 2, and rank of “cba” is 6.

Solution

Let the given string be “STRG”. In the input string, ‘S’ is the first character. There are total 4 characters and 2 of them are smaller than ‘S’. So there can be 2 * 3! smaller strings where first character is smaller than ‘S’, like following:

G X X X
R X X X

Repeat the same process for T, and we get:

Rank = 2*3! + 2*2! + 1*1! + 0*0! = 17

Code

public int getRank(String input) {
    if (input == null || input.length() == 0) {
        return 0;
    }
    input = input.toUpperCase();
    return helper(input) + 1;
}

public int helper(String input) {
    if (input == null || input.length() == 0) {
        return 0;
    }
    char headChar = input.charAt(0);
    int countSmallerThanHead = 0;
    for (char ch : input.toCharArray()) {
        if (ch < headChar) {
            countSmallerThanHead++;
        }
    }
    return countSmallerThanHead * Common.factorial(input.length() - 1)
            + helper(input.substring(1));
}

Question

link

Find the nodes at d distance from a certain node in a Binary Tree

Solution

There are two types of nodes to be considered:

1. Nodes in the subtree rooted of the target node.
2. Other nodes, may be an ancestor of target, or a node in some other subtree.

The details of find these nodes:

1. Find the nodes which can be reached in k hops from the given node.

2. Second part we look at those nodes on the upper part of the tree. The parent of the given node is 1 hop away. Hence in the other child subtree of the parent, we find nodes with k-1 hops.

   Similarly the grand parent of B, we find nodes with k - 2 distance.

Implementation:

1. Start from root, store all nodes in a queue of maximum size k till you reach the given node.

2. Call FindNodesAtDistance() on the nodes from the queue to get all the nodes distance k -i from the node.

Blocking Queue Implementation

source

1. A blocking queue is a queue, so we init a queue with a pre-defined size.

2. BlockingQueue Class comes with Java 5, in java.util.concurrent.BlockingQueue. This example is only used to help you understand what’s happening behind the scene.

3. Both enqueue(Object o){} and dequeue(){} are synchronized method.

4. Both methods do while { wait(); } and then notifyAll().

Code

public class MyBlockingQueue {

    private List<Object> queue = new LinkedList<Object>();
    private int size = 10;

    public MyBlockingQueue(int size) {
        this.size = size;
    }

    public synchronized void enqueue(Object item) throws InterruptedException {
        while (this.queue.size() == this.size) {
            wait();
        }
        if (this.queue.size() == 0) {
            notifyAll();
        }
        this.queue.add(item);
    }

    public synchronized Object dequeue() throws InterruptedException {
        while (this.queue.size() == 0) {
            wait();
        }
        if (this.queue.size() == this.size) {
            notifyAll();
        }

        return this.queue.remove(0);
    }

    public boolean isEmpty() {
        return this.queue.isEmpty();
    }
}

Another example

This BlockingQueue example makes use MyBlockingQueue that we defined above.

public class Main {

    public static void main(String[] args) throws Exception {

        MyBlockingQueue queue = new MyBlockingQueue(1024);

        Producer producer = new Producer(queue);
        Consumer consumer = new Consumer(queue);

        new Thread(producer).start();
        new Thread(consumer).start();

        Thread.sleep(4000);
    }
}

Producer

public class Producer implements Runnable {

    protected MyBlockingQueue queue = null;

    public Producer(MyBlockingQueue queue) {
        this.queue = queue;
    }

    public void run() {
        System.out.println("Producer starting... ");
        try {
            for (int i = 1; i <= 5; i++) {
                queue.enqueue("" + i);
                Thread.sleep(500);
            }
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }
}

Consumer

public class Consumer implements Runnable {

    protected MyBlockingQueue queue = null;

    public Consumer(MyBlockingQueue queue) {
        this.queue = queue;
    }

    public void run() {
        try {
            for (int i = 1; i <= 5; i++) {
                System.out.println(queue.dequeue());
            }
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
        System.out.println("Consumer finished. ");
    }
}

Output:

Producer starting... 
1
2
3
4
5
Consumer finished. 

Overview

A blocking queue is a queue that blocks when you try to dequeue from a empty queue, or if you try to enqueue items into a full queue.

Details

1. BlockingQueue doesn’t accept null values. Otherwise throw NullPointerException.

2. BlockingQueue implementations are thread-safe. All queuing methods are atomic in nature and use internal locks or other forms of concurrency control.

3. BlockingQueue interface is part of java collections framework and it’s primarily used for implementing producer consumer problem.

Two important methods:

1. put(E e): This method is used to insert elements to the queue, if the queue is full it waits for the space to be available.

2. E take(): This method retrieves and remove the element from the head of the queue, if queue is empty it waits for the element to be available.

Usage

BlockingQueue is typically used to have one thread produce objects, with another thread consumes (producer consumer problem). Refer to [Design] Producer Consumer Problem.

Example 1

This example shows how changing the speed of consuming and producing results in different sequence of outputs, using a BlockingQueue. The size of the BlockingQueue is initialized at 5.

public class Main {

    // original post from:
    // http://www.journaldev.com/1034/java-blockingqueue-example-implementing-producer-consumer-problem

    private static final Setting testFullQueue = new Setting(3, 10, 0);
    private static final Setting testEmptyQueue = new Setting(10, 3, 100);

    public static void main(String[] args) {

        // Creating BlockingQueue of size 5
        BlockingQueue<Message> queue = new ArrayBlockingQueue<>(5);

        Setting variableSetting = testFullQueue;
        Producer producer = new Producer(queue, variableSetting.produceSpeed);
        Consumer consumer = new Consumer(queue, variableSetting.consumeSpeed,
                variableSetting.consumerDelay);

        // starting producer to produce messages in queue
        new Thread(producer).start();

        // starting consumer to consume messages from queue
        new Thread(consumer).start();

        System.out.println("Producer and Consumer has been started");
    }

    static class Setting {
        int produceSpeed;
        int consumeSpeed;
        int consumerDelay;

        public Setting(int a, int b, int c) {
            this.produceSpeed = a;
            this.consumeSpeed = b;
            this.consumerDelay = c;
        }
    }
}

Producer

public class Producer implements Runnable {

    private BlockingQueue<Message> queue;
    int produceSpeed;

    public Producer(BlockingQueue<Message> q, int a) {
        this.queue = q;
        this.produceSpeed = a;
    }

    @Override
    public void run() {
        // produce messages
        for (int i = 0; i < 13; i++) {
            Message msg = new Message("" + i);
            try {
                Thread.sleep(produceSpeed);
                queue.put(msg);
                System.out.println("Produced " + msg.getMsg() + "           ("
                        + queue.size() + " items)");
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
        }
        // adding exit message
        Message msg = new Message("exit");
        try {
            queue.put(msg);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }

}

Consumer

public class Consumer implements Runnable {

    private BlockingQueue<Message> queue;
    int consumeSpeed;
    int consumerDelay;

    public Consumer(BlockingQueue<Message> q, int a, int b) {
        this.queue = q;
        this.consumeSpeed = a;
        this.consumerDelay = b;
    }

    @Override
    public void run() {
        try {
            // initial delay: used to wait for producer to
            // fill up the queue
            Thread.sleep(consumerDelay);
            Message msg;
            // consuming messages until exit message is received
            while ((msg = queue.take()).getMsg() != "exit") {
            System.out.println("         " + msg.getMsg() + " Consumed"+ "  ("
                    + queue.size() + " items)");
                Thread.sleep(consumeSpeed);
            }
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
        System.out.println("Consumer finished working. Exit. ");
    }
}

Message Class

public class Message {
    private String msg;

    public Message(String str){
        this.msg=str;
    }

    public String getMsg() {
        return msg;
    }
}

Output (testFullQueue):

Producer and Consumer has been started
Produced 0           (0 items)
         0 Consumed  (0 items)
Produced 1           (1 items)
Produced 2           (2 items)
         1 Consumed  (1 items)
Produced 3           (2 items)
Produced 4           (3 items)
Produced 5           (4 items)
         2 Consumed  (3 items)
Produced 6           (4 items)
Produced 7           (5 items)
         3 Consumed  (5 items)
Produced 8           (5 items)
         4 Consumed  (4 items)
Produced 9           (5 items)
         5 Consumed  (4 items)
Produced 10           (5 items)
         6 Consumed  (4 items)
Produced 11           (5 items)
         7 Consumed  (4 items)
Produced 12           (5 items)
         8 Consumed  (4 items)
         9 Consumed  (4 items)
         10 Consumed  (3 items)
         11 Consumed  (2 items)
         12 Consumed  (1 items)
Consumer finished working. Exit. 

Output (testEmptyQueue):

Producer and Consumer has been started
Produced 0           (1 items)
Produced 1           (2 items)
Produced 2           (3 items)
Produced 3           (4 items)
Produced 4           (5 items)
Produced 5           (5 items)
         0 Consumed  (5 items)
         1 Consumed  (4 items)
         2 Consumed  (3 items)
Produced 6           (4 items)
         3 Consumed  (3 items)
         4 Consumed  (2 items)
Produced 7           (3 items)
         5 Consumed  (2 items)
         6 Consumed  (1 items)
         7 Consumed  (0 items)
Produced 8           (1 items)
         8 Consumed  (0 items)
Produced 9           (1 items)
         9 Consumed  (0 items)
Produced 10           (1 items)
         10 Consumed  (0 items)
Produced 11           (0 items)
         11 Consumed  (0 items)
Produced 12           (1 items)
         12 Consumed  (0 items)
Consumer finished working. Exit. 

Blocking Queue VS. Thread Pool

These are 2 very different things, however it might be a little bit confusing for a layman. I have very little knowledge about Java multi-threading. But after writing some example of thread pool and blockingqueue, I am able to identify some significant differences between the 2 DS:

1. Thread pools are often used in multi threaded servers. For example, we create 10 thread only for processing 1,000 tasks. However in BlockingQueue, there’re typically only 2 thread: Producer and Consumer. Of course there can be more, but the basic pattern defines only 2 (types of) threads.

2. Threads are added into thread pool, while in BlockingQueue, it stores tasks (runnables).

It’s not a common practise to compare the 2 DS. If you read this and have got some interesting thoughts, do not hesitate to let me know by commenting below!

Question

link

Given a digit ‘3141592653’, find number of occurence of subsequence “123”. Note that the sequence occurs twice:

3141592653
 1    2  3
   1  2  3

Output 2.

Solution

Refer to [LeetCode 115] Distinct Subsequences.

Question

link

Find the number of distinct subsequences of a string (include “” as a subsequence).

For example, Input

AAA 
ABCDEFG 
CODECRAFT 

Output

4 
128 
496 

Solution

In [LeetCode 115] Distinct Subsequences, we discuss finding occurence of a given subsequence.

Now if we do not specify a subsequence, we want the total number of distinct subsequence.

The solution is DP, with the following equation:

Let, 

dp[i] = number of distinct subsequences ending with a[i]

last[i] = last position of character i in the given string.

Equation:

dp[i] = dp[last[i] - 1] + ... + dp[i - 1]

The final result is:

Distinct Subsequences = dp[1] + ... dp[len - 1]

Example 1:

Input   : - A B C
dp array: 1 1 2 4
Total = 8

Example 2:

Input   : - A A C
dp array: 1 1 1 3
Total = 6

The code is posted below.

Optimize Solution

There is a good optimization of this DP solution, which is to keep another dp array ‘sum’, which sum[i] = dp[1] + dp[2] + … + dp[i]. The final answer would be sum[len - 1].

This nice idea is from this post. Credit goes to IVlad.

Code

un-optimized code. calculate dp[0] … dp[n], then sum to final result.

public int countDistinctSubseq(String input) {
    int len = input.length();
    int[] dp = new int[len + 1];
    // dp[i] denotes the number of distinct subseq within first 'i' chars
    dp[0] = 1;
    // the first 0 chars is "" - we consider it as 1 subseq

    for (int i = 1; i <= len; i++) {
        // set dp[i]
        // dp[i] = dp[i-1] + ... + dp[k] where input{k} == input{i}
        int p = i - 1;
        while (p >= 0) {
            dp[i] += dp[p];
            if (p > 0 && input.charAt(p - 1) == input.charAt(i - 1)) {
                // when meeting a same char ahead of position i, stop
                // adding to dp[i]
                break;
            }
            p--;
        }
    }
    int sum = 0;
    for (int i : dp) {
        sum += i;
    }
    return sum;
}