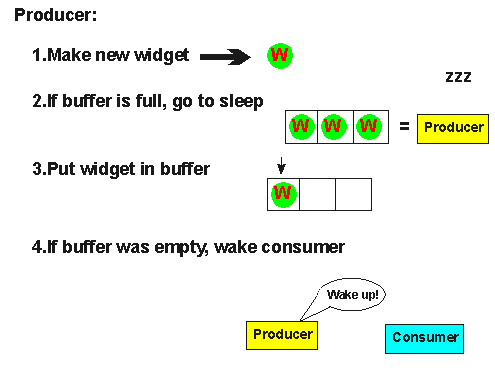
Overview
Thread pool is a collection of managed threads usually organized in a queue, which execute the tasks in the task queue.
Thread pool is a group of pre-instantiated, idle threads which stand ready to be given work.
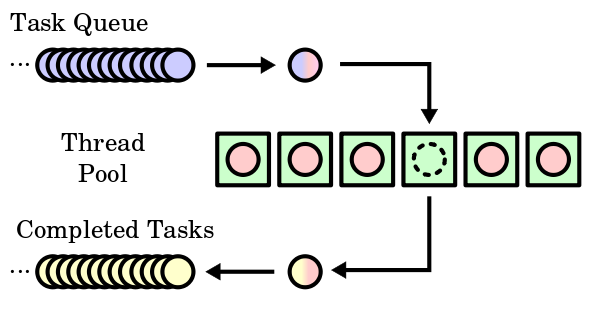
A sample thread pool (green boxes) with waiting tasks (blue) and completed tasks (yellow)
Why Thread Pool?
Thread Pools are useful when you need to limit the number of threads running in your application at the same time.
Thread pools are often used in multi threaded servers. Each connection arriving at the server via the network is wrapped as a task and passed on to a thread pool. The threads in the thread pool will process the requests on the connections concurrently.
Many server applications, such as Web servers (eg. Tomcat), database servers, file servers, or mail servers must process a large number of tasks received from a network protocol. Often, the task is short-lived and the number of requests is large.
Instead of starting a new thread for every task to execute concurrently, the task can be passed to a thread pool. As soon as the pool has any idle threads the task is assigned to one of them and executed.
Implementation
This is a simple thread pool implementation. The pool is implemented using a list of tasks, and a list of threads. Theads will fetch tasks and run it. The list is implemented with a BlockingQueue - however, it’s fine to use just a normal queue.
Main Class:
public class Main {
public static void main(String[] args) {
// In this example, we create 3 thread to run 10 tasks
// set the BlockingQ size to be 5.
ThreadPool tp = new ThreadPool(3, 5);
List<MyTask> todoList = new ArrayList<MyTask>();
for (int i = 1; i <= 10; i++) {
todoList.add(new MyTask("T" + i));
}
for (MyTask todo : todoList) {
tp.execute(todo);
}
while (!tp.noMoreTask()) {
try {
Thread.sleep(2000);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
tp.stop();
}
}
Pool Class:
public class ThreadPool {
// a list of tasks (BlockingQueue)
// a list of thread
private MyBlockingQueue taskQueue = null;
private List<MyThread> threads = new ArrayList<MyThread>();
private boolean isStopped = false;
public ThreadPool(int numThreads, int maxNumTasks) {
taskQueue = new MyBlockingQueue(maxNumTasks);
for (int i = 0; i < numThreads; i++) {
threads.add(new MyThread(taskQueue));
}
System.out.println("Thread pool initiated. ");
for (MyThread thread : threads) {
thread.start();
}
}
public synchronized void execute(Runnable task) {
if (this.isStopped) {
throw new IllegalStateException("ThreadPool is stopped");
}
try {
this.taskQueue.enqueue(task);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
public boolean noMoreTask() {
return this.taskQueue.isEmpty();
}
public synchronized void stop() {
this.isStopped = true;
for (MyThread thread : threads) {
// thread.stop();
thread.interrupt();
}
System.out.println("Thread pool stopped. ");
}
}
Thread Class:
public class MyThread extends Thread {
private MyBlockingQueue taskQueue = null;
private boolean isStopped = false;
public MyThread(MyBlockingQueue queue) {
taskQueue = queue;
}
public void run() {
while (!isStopped()) {
try {
Runnable runnable = (Runnable) taskQueue.dequeue();
runnable.run();
} catch (Exception e) {
// log or otherwise report exception,
// but keep pool thread alive.
}
}
}
// public synchronized void stop() {
// isStopped = true;
// this.interrupt(); // break pool thread out of dequeue() call.
// }
public synchronized boolean isStopped() {
return isStopped;
}
}
Task Class:
public class MyTask implements Runnable {
String message;
public MyTask(String s) {
message = s;
}
@Override
public void run() {
// do some task here...
// finish the task ...
System.out.println("Task finished: " + message);
}
}
Output:
Thread pool initiated.
Task finished: T1
Task finished: T3
Task finished: T4
Task finished: T5
Task finished: T6
Task finished: T2
Task finished: T7
Task finished: T10
Task finished: T9
Task finished: T8
Thread pool stopped.